Knowing mental arithmetic shortcuts can make calculating your course to steer quick and simple, says Peter Strike
Basic skills in mental arithmetic can be very useful in navigation and course to steer planning, writes Peter Strike.
They are also very useful in pilotage and watch-keeping, not to mention anchoring.
The Royal Navy is very good at recognising people’s general weakness in maths, and has established a number of practices to make life easy.
Dead reckoning
A simple example is the DR (dead reckoning) plot, usually plotted at six-minute intervals for coastal navigation except in pilotage waters when it is every three minutes (remember, a fix is history, it is the DR that keeps you safe by looking ahead).
Why every six minutes you might ask, how does that make life simple? Six minutes is one tenth of an hour (60 minutes).
Maintaining a DR plot lets you know where you will be, not just where you’ve been
If you are travelling at 12 knots, how far have you travelled in six minutes? The answer? 1.2 miles. Simply divide the speed by 10, shift the decimal point one place to the left.
Anyone can manage that. Then DR ahead at 1.2 mile intervals, marking the time increasing by six minutes for each DR line.
If you obtain a fix at 0930, and DR ahead for 3 x 6 minute intervals, all being well you now know you are safe until 0948 (Diagram 1).
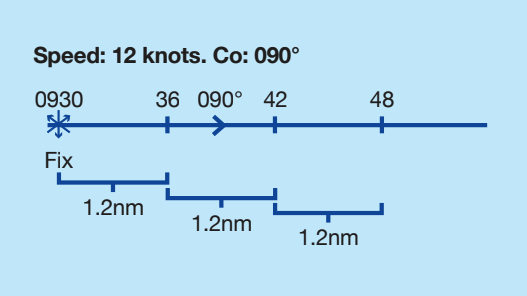
Diagram 1. Credit: Maxine Heathj
Course to steer
One method requires you to divide 60 by your boat speed, and then multiply this by the rate of tide in order to calculate a course to steer.
This is correct of course, but how to do this easily?
The answer is to use the clock face rule, a trick widely used also by aeroplane pilots as well as the Royal Navy.
Let’s say you are cruising at 5 knots on a broad reach (little or no leeway) and your tidal atlas or diamond tells you that you will be experiencing a tidal stream on your port beam of 2.5 knots (Diagram 2).
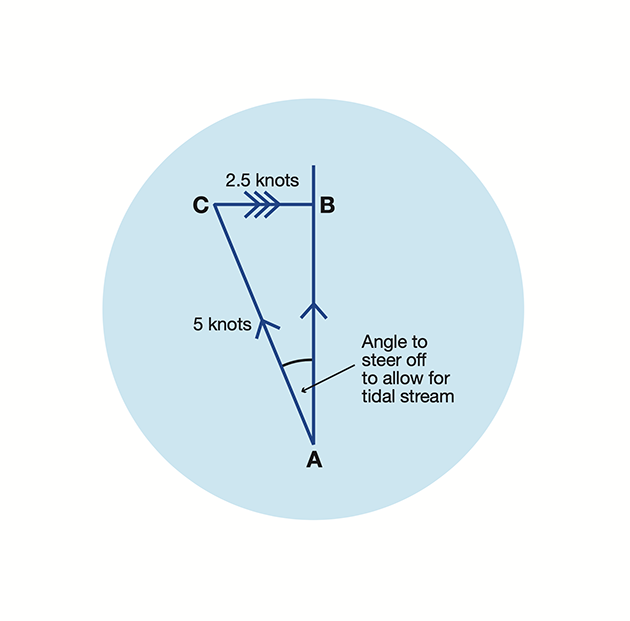
Diagram 2. Knowing the sine rule will let you calculate the angle for your course correction quickly. Credit: Maxine Heath
You want to know how far to steer off (angle BAC, course AC) to make good the course you need (course AB).
The conventional approach says draw a triangle, plot a line representing your speed (5 knots, AC; plot a line representing the tidal flow (2.5 knots, BC).
Join A to C and measure angle BAC.
By the time you have done this, the moment will have passed, and you won’t care what the angle is!
Continues below…
Navigation masterclass: 7 coastline types
No matter where you are in the world, if you are cruising a coast the chances are it will fall…
8 tips for digital navigation
As with all aspects of navigation, following ‘best practice’ is the surest way to make sure you are passage planning…
10 classic pilotage mistakes in navigation…
…and how to avoid them. James Stevens reveals the classic pilotage mistakes and explains what you need to do to…
Celestial navigation: understanding the night sky
You don't need complicated maths or even a sextant to enjoy the night sky and use it for navigation, says…
A bit of mental arithmetic will give you the answer almost immediately.
Think about angle BAC, the angle you want. The sine of angle BAC is given by opposite/hypotenuse or, more simply, the ratio of tidal stream to your speed: 2.5 / 5 = 0.5
The next question is which angle has a sine of 0.5? Forgotten your trigonometric tables? Fortunately you don’t need them.
Use a simple version of the 60 mile/1° rule, namely the clock face rule.
Look at Diagram 3 representing a clock face in hours and minutes.
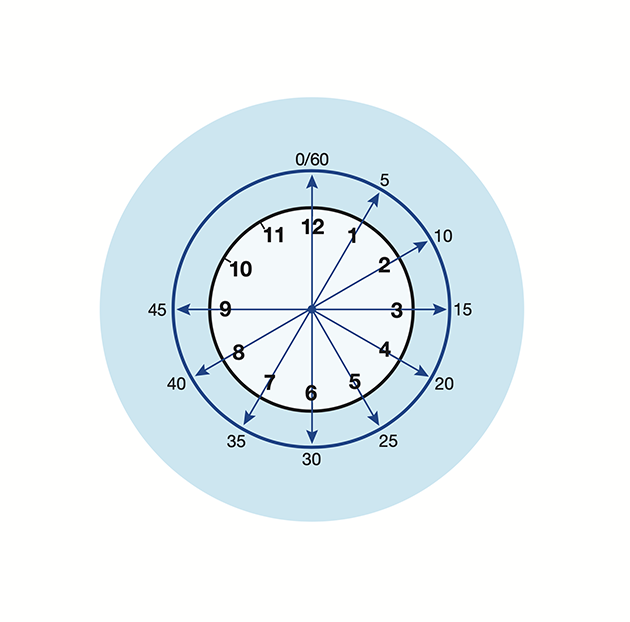
Diagram 3. The clock face rule equates fractions of an hour to angles. Credit: Maxine Heath
The clock face rule says that the angle with a sine of 0.5 is 30; 30 minutes is half an hour, 0.5 of an hour. So angle BAC is 30º.
If the tidal stream had been 1 knot on the beam, the ratio of speed to stream would be 1/5, and on the clock face, a fifth of an hour is 12 minutes.
So you steer of 12º off.
It is an approximation (except for 30 mins/0.5 which is exact) but it is a very good one from dead ahead 0º all the way round to 45º.

If you’re on deck, calculating course to steer corrections in your head can be extremely useful.
Sine 15º is approximately 0.25 (quarter of an hour), sine 20º approximates to 0.33 (third of an hour), since 45º is roughly 0.75 but becomes increasingly inaccurate.
I have shown a very simple case, with the tide on the beam.
It usually isn’t so obliging of course, but you can use exactly the same calculation process to deal with other angles. You just use it twice.
Let’s say the tidal stream is not on your beam, but is 30º on your starboard bow, at 2.5 knots.
Now how much course compensation do you need to make to maintain your course over the ground?
You can break the tidal stream into two components, one pushing you sideways, for which you need to compensate your course, and one from dead ahead, slowing you down (Diagram 4).
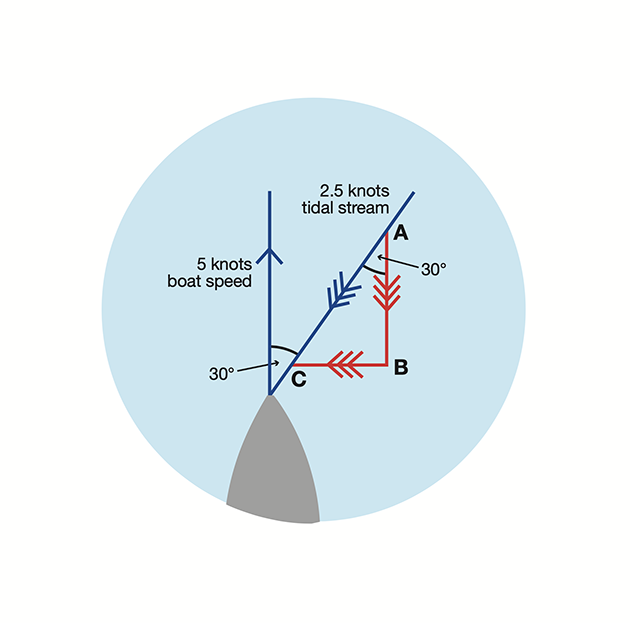
Diagram 4. For other tidal vectors, break it down and use the component on your beam. Credit: Maxine Heath
To make the course correction you need to know the vector on your beam, BC.
You know the hypotenuse, AC (2.5 knots), you know the angle CAB (30º, same as the angle off the bow).
So how long must CB be so that the ratio CB/AC is equal to sin 30º, i.e. 0.5? CB must be half AC, i.e. 1.25. Seems strange doesn’t it?
The tidal stream is at only 30º off your bow, and yet you are being pushed sideways by half of it! How much to steer off then?

Peter Strike is an RYA Yachtmaster Offshore and was senior training officer with the Liverpool URNU (RNR). He sails a Hunter Channel 32 based at Port Edgar
Now we need to make a correction for a tidal stream of 1.25 knots on the beam of our vessel proceeding at 5 knots: 1.25/5 = 0.25 or quarter.
Apply to the clock face – quarter of an hour is 15 minutes, therefore the course correction needed is 15º.
Not as easy as the first example perhaps, but a whole lot quicker than plotting out two vector diagrams.
You can of course, on a longer passage, add all the tidal vectors together, sum them into a single vector and then use the clock face rule.
The same simple trigonometry is also very useful for those on watch and, as has been said, can give the ‘computer in your head’ the chance to calculate the closest point of approach of other vessels, distance off headlands and a variety of other useful information.
It also stops the watch keeper getting bored on a long passage.
Enjoyed reading Course to steer: how to calculate it in your head?
A subscription to Yachting Monthly magazine costs around 40% less than the cover price.
Print and digital editions are available through Magazines Direct – where you can also find the latest deals.
YM is packed with information to help you get the most from your time on the water.
-
-
- Take your seamanship to the next level with tips, advice and skills from our experts
- Impartial in-depth reviews of the latest yachts and equipment
- Cruising guides to help you reach those dream destinations
-
Follow us on Facebook, Twitter and Instagram.









